Question

Ayudenmee plis

El sueldo de los trabajadores de una multinacional sigue una distribución normal con media µ=$2000 y una desviación estándar σ=$600. Si se tomó una muestra de 64 trabajadores, calcular el intervalo de confianza para estimar el sueldo medio poblacional de los trabajadores, con un nivel de confianza del 99%.

Answer 1

El intervalo, con un nivel de confianza de 99%, para estimar el sueldo medio poblacional de los trabajadores es de ($1807, $2193).

Explanation:

El primero paso es el encuentro de lo
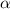`\alpha`, que es la subtracion de 1 por lo nivel de confianza e divididos por 2. Entonces:

`\alpha = (1 - 0.99)/(2) = 0.005`

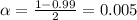
Ahora, buscamos a z en la tabela Z de manera que z tienga uno p-value de
`1 - \alpha`.

Entonces, z con uno p-value de
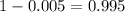`1 - 0.005 = 0.995`, o sea, z = 2.575.

La margen de error es:

`M = z(\sigma)/(√(n))`

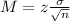
En que
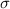`\sigma` es la desviación estándar y n es el tamaño de la muestra.

σ=$600. Si se tomó una muestra de 64 trabajadores

Entonces
`\sigma = 600, n = 64`

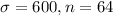
Margen de error:

`M = z(\sigma)/(√(n))`

`M = 2.575(600)/(√(64))`

`M = 193`

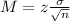
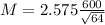
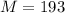
El limite inferior es la subtración de la media de la muestra por la margen de error. Entonces 2000 - 193 = $1807.

El limite inferior es la suma de la media de la muestra con la margen de error. Entonces 2000 + 193 = $2193.

El intervalo, con un nivel de confianza de 99%, para estimar el sueldo medio poblacional de los trabajadores es de ($1807, $2193).