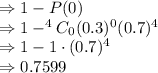Question

Can't find probability​

Answer 1

Answer:
`0.0756,\ 0.7599`

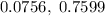
Explanation:

Given

Probability that a coin will land head is
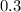`0.3` i.e. probability of success is
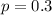`p=0.3` So, the probability of failure is
`q=1-0.3=0.7`

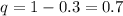
Using Binomial distribution for
`n=4`

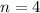
(a) Probability that the coin will lead heads exactly 3 times

`\Rightarrow P(3)=^4C_3(0.3)^3(0.7)^1\\\Rightarrow P(3)=4* 0.7* (0.3)^3\\\Rightarrow P(3)=0.0756`

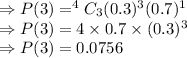
(b)Probability that the coin lands head at least once

`\Rightarrow 1-P(0)\\\Rightarrow 1-^4C_0(0.3)^0(0.7)^4\\\Rightarrow 1-1\cdot(0.7)^4\\\Rightarrow 0.7599`