Answer:
7)
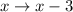 .
.
8)
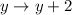
9) The entire quadratic equation did not get reflected.
Explanation:
7) A horizontal translation to the right is of the form:
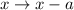
Let
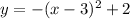 , then the horizontal translation is represented by
, then the horizontal translation is represented by
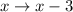 .
.
8) A vertical translation upwards is of the form:

Let
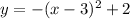 , then the vertical translation is represented by:
, then the vertical translation is represented by:
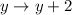
9) The only component of the quadratic equation that was reflected was the part
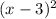 along the x-axis. We can create the entire function by applying the following steps:
along the x-axis. We can create the entire function by applying the following steps:
(i)
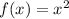 (Original function)
(Original function)
(ii)
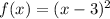 (Horizontal translation)
(Horizontal translation)
(iii)
 (Reflection)
(Reflection)
(iv)
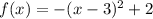 (Vertical translation)
(Vertical translation)
The entire quadratic equation did not get reflected.