Given:
Side of a square = x units
The side of square is decreased by 9 units.
To find:
The expression that represents the area of the new square in square units.
Solution:
It is given that, the side of a square is x units and it is decreased by 9 units. So, the side of new square is:

The area of a square is:
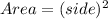
So, the area of the new square is:

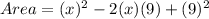
![[\because (a-b)^2=a^2-2ab+b^2]](https://img.qammunity.org/2022/formulas/mathematics/college/5g4f7w0d9ahy69ly1oxw8vqo5n8zn5stjf.png)
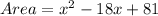
Therefore, the expression for the area of the new square is either
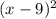 or
or
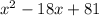 , both are equivalent.
, both are equivalent.