Answer:

Step-by-step explanation:
Given that,
The mass of a Hubble Space Telescope,
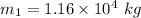
It orbits the Earth at an altitude of

We need to find the potential energy the telescope at this location. The formula for potential energy is given by :

Where
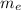 is the mass of Earth
is the mass of Earth
Put all the values,
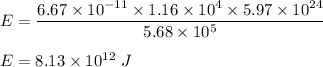
So, the potential energy of the telescope is
 .
.