Question

A 12 ft. ladder is leaning against a house. The ladder makes a 60° angle with the ground. Use special right triangles to find how far up the building the ladder will reach.

Answer 1

Given:

The length of the ladder = 12 ft

The angle of ladder with ground = 60 degrees

To find:

How far up the building the ladder will reach.

Solution:

Using the given information draw a figure as shown below.

We need to find the vertical distance between the top of ladder and the ground.

Let x be the required distance.

In a right angle triangle,

`\sin \theta=(Perpendicular)/(Hypotenuse)`

In the below triangle ABC,

`\sin A=(BC)/(AC)`

`\sin 60^\circ=(x)/(12)`

`(√(3))/(2)=(x)/(12)`

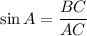
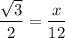
Multiply both sides by 12.

`(√(3))/(2)* 12=x`

`6√(3)=x`

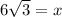
Therefore, the ladder will reach
`6√(3)` ft far up the building.