1 Answer

Dlowe · Answer 1 · 2022-06-16T16:13:38+0000

Given:

The figure of a rhombus QRST.

To find:

A. The value of x.

B. The measure of angle RQP.

Solution:

A. We need to find the value of x.

We know that the diagonals of a rhombus are perpendicular bisectors. It means the angles on the intersection of diagonals are right angles.

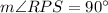$m\angle RPS=90^\circ$ [Right angle]

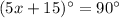
$(5x+15)^\circ=90^\circ$

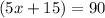
(5x+15)=90

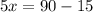
5x=90-15

5x=75

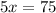
Divide both sides by 5.

x=(75)/(5)

x=15

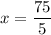
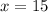
Therefore, the value of x is 15.

B. We need to find the measure of angle RQP.

From the given figure, it is clear that

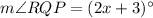
$m\angle RQP=(2x+3)^\circ$

Putting
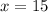x=15 , we get

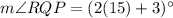
$m\angle RQP=(2(15)+3)^\circ$

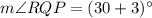
$m\angle RQP=(30+3)^\circ$

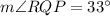
$m\angle RQP=33^\circ$

Therefore, the measure of angle RQP is 33 degrees.

Please log in or register to add a comment.