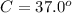Question

Consider a triangle A BC like the one below. Suppose that A = 100°, b =51, and c= 45. (The figure is not drawn to scale.) Solve the triangle. Carry your intermediate computations to at least four decimal places, and round your answers to the nearest tenth. If there is more than one solution, use the button labeled "or".

Answer 1

`A = 100^o`

`B = 43.0^o`

`C =37.0^o`

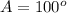
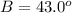
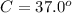
Explanation:

Given

`A = 100^o`

`b = 51`

`c =45`

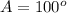
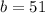
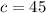
Required

Complete the triangle (See attachment)

First, calculate side a using cosine's equation

`a^2 = b^2 + c^2 -2bc \cos A`

`a^2 = 51^2 + 45^2 -2*51*45 \cos (100^o)`

`a^2 = 4626 -4590 *-0.1736`

`a^2 = 4626+ 796.8`

`a^2 = 5422.8240`

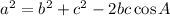
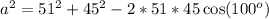
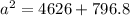
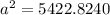
Take square roots

`a = 73.6398`

The measure of B and C can then be calculated using sine's equation

`(a)/(\sin A) =(b)/(\sin B) =(c)/(\sin C)`

So:

`(73.6398)/(\sin (100)) =(51)/(\sin B)`

`(73.6398)/(0.9848) =(51)/(\sin B)`

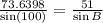
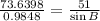
Cross multiply

`\sin B * 73.6398 = 51 * 0.9848`

`\sin B * 73.6398 = 50.2248`

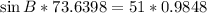
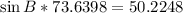
Solve for sin B

`\sin B = (50.2248)/(73.6398)`

`\sin B = 0.6820`

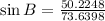
Take arc sin of both sides

`B = \sin^(-1)(0.6820)`

`B = 43.0^o`

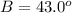
To calculate C, we make use of:

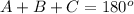`A + B + C = 180^o` --- angles in a triangle

`100 + 43 + C = 180`

`143 + C = 180`

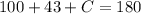
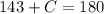
Collect like terms

`C =180-143`

`C =37.0^o`