Question

Create a polynomial function in factored form that crosses through the x-axis at -2 and touches the x-axis and turns around at 4.​

Answer 1

Given:

A polynomial crosses through the x-axis at -2 and touches the x-axis and turns around at 4.​

To find:

The polynomial function in factored form.

Solution:

If the graph of a polynomial intersect the x-axis at
`x=a`, then
`(x-a)` is a factor of the polynomial.

If the graph of a polynomial touches the x-axis at
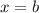`x=b`, then
`(x-b)` is a factor of the polynomial with multiplicity 2. In other words
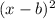`(x-b)^2` is the factor of the polynomial.

It is given that the polynomial crosses through the x-axis at -2. So,
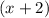`(x+2)` is a factor of required polynomial.

It is given that the polynomial touches the x-axis and turns around at 4. So,
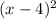`(x-4)^2` is a factor of required polynomial.

Now, the required polynomial is:

`P(x)=(x+2)(x-4)^2`

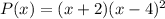
Therefore, the required polynomial is
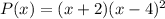`P(x)=(x+2)(x-4)^2`.