Question

Triangle ABC has vertices A(- 3, - 4), B(16, - 2) and C(13, - 10) . Show algebraically that ABC is a right angled triangle.​

Answer 1

Given:

The vertices of a triangle ABC are A(-3,-4), B(16,-2) and C(13,-10).

To show:

That the triangle ABC is a right angled triangle.​

Solution:

Distance formula:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

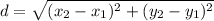
The vertices of a triangle ABC are A(-3,-4), B(16,-2) and C(13,-10).

Using the distance formula, we get

`AB=√((16-(-3))^2+(-2-(-4))^2)`

`AB=√((19)^2+(2)^2)`

`AB=√(361+4)`

`AB=√(365)`

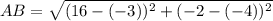
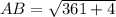
Similarly,

`BC=√(\left(13-16\right)^2+\left(-10-\left(-2\right)\right)^2)`

`BC=√(73)`

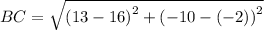
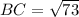
And,

`AC=√(\left(13-\left(-3\right)\right)^2+\left(-10-\left(-4\right)\right)^2)`

`AC=√(292)`

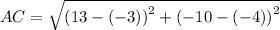
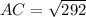
Now, add the square of two smaller sides.

`BC^2+AC^2=(√(73))^2+(√(292))^2`

`BC^2+AC^2=73+292`

`BC^2+AC^2=365`

`BC^2+AC^2=(AB)^2`

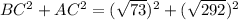
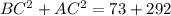
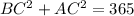
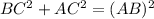
Since the sum of the square of two smaller sides is equal to the square of the largest side, therefore the given triangle is a right angle triangle by using Pythagoras theorem.

Hence proved.