Question

2x-y=-1 , 3x-y=2 solve by substition

Answer 1

x = 3, y = 7

or (3,7)

Explanation:

We are given the system of equations below:

`\large{ \begin{cases} 2x - y = - 1 \\ 3x - y = 2 \end{cases}}`

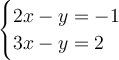
We are required to solve the system by substitution method. What we have to do is to isolate either x-term or y-term so we can use the method. I will be isolating y-term because it is faster due to having 1 as a coefficient.

By isolating y-term, just pick one of the given equations to isolate. No need to isolate the whole system. (I will be isolating y-term of the first equation.)

`\large{ \begin{cases} y= 2x + 1\\ 3x - y = 2 \end{cases}}`

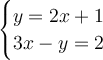
Then we substitute y = 2x+1 in the second equation.

`\large{3x - (2x + 1) = 2}`

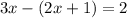
Use the distribution property.

`\large{3x - 2x - 1 = 2}`

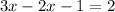
Isolate x-term to solve the equation.

`\large{x = 2 + 1} \\ \large{x = 3}`

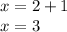
Since we are solving a system of equations. We have to solve for both x-value and y-value to complete. We have already found x-value, but nor y-value yet. Therefore, our next step is to substitute the value of x that we solved in any given equations. It's recommended to substitute in an equation that doesn't have high coefficient value. So I will be substituting x = 3 in the first equation.

`\large{2x - y = - 1} \\ \large{2(3) - y = - 1} \\ \large{6 - y = - 1}`

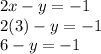
Isolate and solve for y-term.

`\large{6 + 1 = y} \\ \large{7 = y} \\ \large{y = 7}`

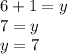
Since we substitute x = 3 and get y = 7. We can write in ordered pairs as (3,7)

Hence, the solution is (3,7)