Question

PLZ HELP, DUE TONIGHT!! Find the values of a and b such that f(x) is continuous at x=

Answer 1

Answers:

a = 2 and b = -4

============================================================

Step-by-step explanation:

Let's define the three helper functions

• f(x) = ax^2 - b
• h(x) = 6
• j(x) = 5ax+b

which are drawn from the piecewise function. The g(x) function will change depending on what the input is.

• If x < 1, then g(x) = f(x).
• If x = 1, then g(x) = h(x)
• If x > 1, then g(x) = j(x)

Since we want g(x) to be continuous at x = 1, this must mean the three functions f(x), h(x), j(x) must have the same output value when the input is x = 1.

Because h(x) = 6 is a constant function, the output is always 6 regardless of the input. Therefore, we want f(x) and j(x) to have 6 as their output when x = 1. Or else, the pieces won't connect.

Plug x = 1 into the f(x) function to get

f(x) = ax^2 - b

f(1) = a(1)^2 - b

f(1) = a - b

Set this equal to the desired output of 6 and we end up with the equation a-b = 6. Solving for 'a' leads to a = b+6.

------------

We'll use the same idea for j(x)

j(x) = 5ax + b

j(1) = 5a(1) + b

j(1) = 5a + b

5a+b = 6

5(b+6) + b = 6 ... plug in a = b+6; solve for b

5b+30+b = 6

6b+30 = 6

6b = 6-30

6b = -24

b = -24/6

b = -4

Which then leads to,

a = b+6

a = -4+6

a = 2

------------

Since a = 2 and b = -4, we go from this

`g(x) = \begin{cases}ax^2-b, \ \ x < 1\\6, \ \ x = 1\\5ax+b, \ \ x > 1\end{cases}`

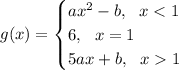
to this

`g(x) = \begin{cases}2x^2+4, \ \ x < 1\\6, \ \ x = 1\\10x-4, \ \ x > 1\end{cases}`

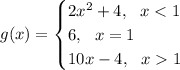
Meaning

f(x) = 2x^2+4 and j(x) = 10x-4

You should find that plugging x = 1 into each of those two functions leads to 6 as the output.

The graph is shown below. Note the red graph f(x) is only drawn when x < 1. Similarly, j(x) is only drawn when x > 1. The orange point represents h(x) which only happens when x = 1. So as the name implies, the piecewise function g(x) is composed of pieces of the three functions f(x), h(x), j(x).