Question

There's a width of 8 in., a length of 20 in., and a height of 12 in.

a) what is the longest poster you could fit in the box? express your answer to the nearest tenth of an inch.
b) explain why you can fit only one maximum-length poster in the box, but you can fit multiple 21.5-inch posters in the same box.

Answer 1

a.

Approximately
`24.7\; \rm in`.

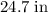b.

While there are three diagonals in a box (a rectangular prism,) all three diagonals goes through the same point- the centroid of this box.

For a maximum-length poster to fit in this box, it would have to be on one of the main diagonals of this box. Hence, any maximum-length poster that fits in this box would go through the centroid of this box.

It's not possible to force more than one posters to go through the same point (i.e., the centroid) in space. Hence, it would not be possible to fit a second maximum-length poster into this box.

This argument does not apply to
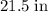`21.5\; \rm in` posters. These posters are shorter than the diagonal of this box; they could fit inside the box without having to go through a particular point in space.

Explanation:

The longest poster that could be fit into this box (a rectangular prism) would be as long as the longest line segment in this box. That line segment would be one of the three diagonals of this box.

Apply the Pythagorean theorem twice to find the length of that diagonal.

Start by finding calculating the diagonal of the base of this box. The base of this box is a rectangle with width
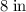`8\; \rm in` and length
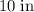`10\; \rm in`. The length of its diagonal would be
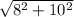`√(8^2 + 10^2)` inches.

Combine that with the height of this box to find the length of the diagonal of this box.

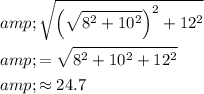`\begin{aligned}& \sqrt{{\left(√(8^2 + 10^2)\right)}^2 + 12^2 \\ &= √(8^2 + 10^2 + 12^2) \\ &\approx 24.7 \end{aligned}`.