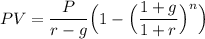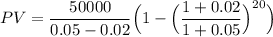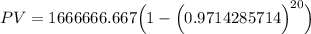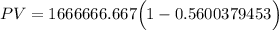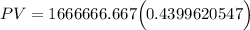Answer:
PV = $733,271
Step-by-step explanation:
From the given information:
The annual payment (P) = $50,000
number of years (n) = 20
The growth percentage = 2% = 0.02
Rate of percentage earned = 5% = 0.05
Using the formula illustrated below to determine the Present Value (PV) of a growing annuity;