Question

A drawer contains black socks and white socks. A person randomly selects two socks without replacement. The probability of selecting two black socks is 120703 and the probability of selecting a black sock on the first draw is 819. What is the probability of selecting a black sock on the second draw given that a black sock was selected on the first draw

Answer 1

0.4054 = 40.54% probability of selecting a black sock on the second draw given that a black sock was selected on the first draw

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

In which

P(B|A) is the probability of event B happening, given that A happened.

`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

In this question:

Event A: Black sock on the first draw.

Event B: Black sock on the second draw.

The probability of selecting a black sock on the first draw is 8/19.

This means that
`P(A) = (8)/(19)`

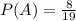
Black socks on both draws:

The probability of selecting two black socks is 120/703

This means that
`P(A \cap B) = (120)/(703)`

What is the probability of selecting a black sock on the second draw given that a black sock was selected on the first draw?

`P(B|A) = (P(A \cap B))/(P(A))`

`P(B|A) = ((120)/(703))/((8)/(19))`

`P(B|A) = (120)/(703)*(19)/(8)`

`P(B|A) = (120*19)/(703*8)`

`P(B|A) = 0.4054`

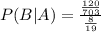
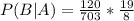
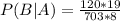
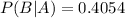
0.4054 = 40.54% probability of selecting a black sock on the second draw given that a black sock was selected on the first draw