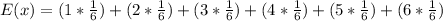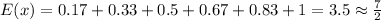Question

1) A traditional die is a cube with each of its six sides representing the numbers from 1 to 6. Mr. Dicey customized a die by replacing each number with its reciprocal (reciprocal of x is 1/x ). What is the expected value if you roll the customized die for 6 times?

2) A game is played by throwing 3 dice. You will win in this game if the summation of the scores of these 3 dice is 3, 4, 17, 18.

What is the variance of your expected values?

3) Two dice are rolled. [A die has six sides, each representing the score from 1 to 6]

What is the expected value if you roll these two dice for 6 times?

Answer 1

1)
`(2)/(5)`

2) 49.225

3)
`(7)/(2)`

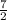
Explanation:

1) To find the expected value of the dice we can use the following equation:

`E(x)=x_(1)*P(x_(1))+x_(2)*P(x_(2))+...+x_(n)*P(x_(n))`

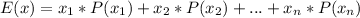
So in our problem the values x will be: 1/1, 1/2, 1/3, 1/4, 1/5 and 1/6 and the probavility for all values is 1/6 so the expected values will be:
`E(x)=((1)/(1) *(1)/(6)) +((1)/(2) *(1)/(6)) +((1)/(3) *(1)/(6))+((1)/(4) *(1)/(6))+((1)/(5) *(1)/(6))+((1)/(6) *(1)/(6))`

`E(x)=0.167+0.083+0.056+0.042+0.033+0.028=0.409\approx (2)/(5)`

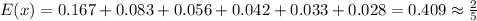
2) To find the variance of the expected values we can use the equation:

`Var(x)=\frac{\sum_(i=1)^(n)(x_(i)-\overline{x})^(2) }{n}`

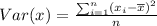
So for our problem will be:

`Var(x)=((3-10.5)^2+(4-10.5)^2+(17-10.5)^2+(18-10.5)^2)/(4)`

`Var(x)=(56.25+42.25+42.25+56.25)/(4)`
`Var(x)=(196.9)/(4)=49.225`

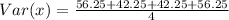
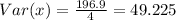
3) To find the expected value of the dice we can use the following equation:

`E(x)=x_(1)*P(x_(1))+x_(2)*P(x_(2))+...+x_(n)*P(x_(n))`

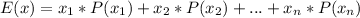
So in our problem the values x will be: 1, 2, 3, 4, 5 and 6 and the probavility for all values is 1/6 so the expected values will be:
`E(x)=(1*(1)/(6)) +(2 *(1)/(6)) +(3 *(1)/(6))+(4 *(1)/(6))+(5 *(1)/(6))+(6 *(1)/(6))`

`E(x)=0.17+0.33+0.5+0.67+0.83+1=3.5\approx (7)/(2)`