Answer:
She will be going at 11.01 m/s when she reaches the bottom.
Step-by-step explanation:
We can find the speed at the bottom by equating the total work with the change in energy:
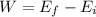 (1)
(1)
There is no energy conservation because there is a force of friction on her way down.
By entering
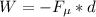 , where
, where
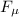 is the force of friction (is negative because it is in the opposite direction of motion) and d is the displacement, into equation (1) we have:
is the force of friction (is negative because it is in the opposite direction of motion) and d is the displacement, into equation (1) we have:
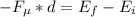
In the initial state, we have kinetic and potential energy and in the final state, we have only kinetic energy.

Where:
m: is the total mass = 40 kg
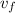 : is the final speed =?
: is the final speed =?
 : is the intial speed = 5 m/s
: is the intial speed = 5 m/s
g: is the gravity = 9.81 m/s²
h: is the height = 10 m

By solving the above equation for
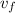 we have:
we have:
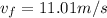
Therefore, she will be going at 11.01 m/s when she reaches the bottom.
I hope it helps you!