Question

13. In isosceles triangle HMS, ZM is the vertex angle.

If m2M = (2x + 6)° and mZH (9x + 7)º, what

is mZM?

A. 10°

B. 22°

C. 79°

D. 80°

Answer 1

B.
`22^(\circ)`

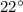
Explanation:

We are given that HMS is an isosceles triangle.

Angle M is the vertex angle.

`m\angle M=(2x+6)^(\circ)`

`m\angle H=(9x+7)^(\circ)`

`\angle H=\angle S`

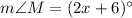
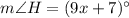
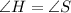
By definition of isosceles triangle

We have to find the measure of angle M.

`\angle M+\angle H+\angle S=180^(\circ)`

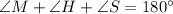
By using sum of angles of triangle property

Substitute the values

`2x+6+9x+7+9x+7=180`

`20x+20=180`

`20x=180-20`

`20x=160`

`x=(160)/(20)=8`

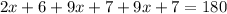
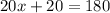
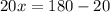
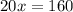
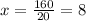
Using the value of x

`m\angle M=2(8)+6`

`m\angle M=22^(\circ)`

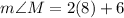
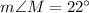
Hence, option B is correct.