Given:
The quadratic equation is:
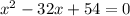
It can be written as
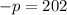 .
.
To find:
The value of p in the rewritten equation.
Solution:
We have,
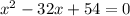
Isolate the constant term.
We need to make 202 on the right side. So, add 256 on both sides.
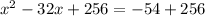
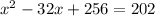
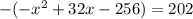
Let
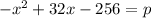 , then
, then
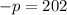
Therefore, the value of p is
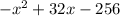 .
.
The given equation can be written as:
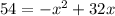
Adding 148 on both sides, we get
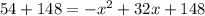
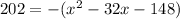
Let
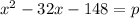 , then
, then
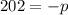
Therefore, the another possible value of p is
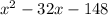 .
.