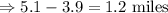Question

20. Jeremy likes to ride his bike to his friend Khaleel's

house. If he takes the road, he rides 3.6 miles east

and then 1.5 miles north. There is also a path that

goes through the woods directly from Jeremy's

house to Khaleel's house.

Part A. To the nearest degree, what is the angle

shown between the road and the path?

Part B. To the nearest tenth of a mile, how much

farther is it to go by the road than to go by the

path?

Answer 1

Answer:
`22.62^(\circ),1.2\ \text{miles}`

Explanation:

Given

Jeremy takes road and ride 3.6 miles to the east and then 1.5 miles to the north

If there is a path that goes through the woods directly from Jeremy's house to Khaleel's house with length x(say)

From the figure, we can write the angle between road and the path

`\Rightarrow \tan \theta=(1.5)/(3.6)\\\\\Rightarrow \tan \theta=0.4167\\\Rightarrow \theta=22.62^(\circ)`

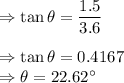
(b)Length of the path is

`\Rightarrow x=√(3.6^2+1.5^2)\\\Rightarrow x=√(15.21)\\\Rightarrow x=3.9\ miles`

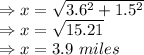
Distance covered by the road is
`3.6+1.5=5.1\ miles`

Difference between the two lengths is

`\Rightarrow 5.1-3.9=1.2\ \text{miles}`