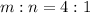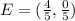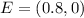Question

Plot c so its distance from the origin is 1. Plot poin e 4/5 closer to the origin than c. What is its cooridinate?

Answer 1

`C = (1,0)`

`E = (0.8,0)`

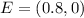
See attachment for C and E

Explanation:

Given

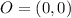`O= (0,0)` --- Origin

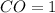`CO = 1` --- distance of C to O

Solving (a): Plot point C

Calculate the coordinates of C using distance formula:

`d = √((x_2 - x_1)^2 + (y_2 -y_1)^2)`

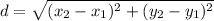
Where:

`O= (0,0)` ---
`(x_1,y_1)`

`C = (x,y)` --
`(x_2,y_2)`

`d = CO = 1`

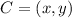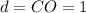
So, we have:

`1 = √((x - 0)^2 + (y -0)^2)`

`1 = √(x^2 + y^2)`

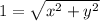
Square both sides

`1^2 = x^2 + y^2`

`x^2 + y^2 =1`

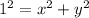
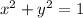
For this solution, we assume y = 0

`x^2 + 0^2 =1`

`x^2=1`

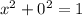
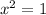
Solve for x

`x = 1`

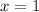
So, the coordinates of C is: (1,0)

`C = (1,0)`

Solving (b): Plot point E

We have that E is 4/5 closer to the origin.

This implies that, the ratio is:

`m : n = 4/5:1/5`

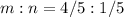
Multiply by 5

`m : n = 4:1`

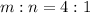
So, E is at 4:1 between O and C

Calculate the coordinates of E using:

`E = ((mx_2 + nx_1)/(m + n),(my_2 + ny_1)/(m + n))`

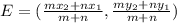
Where

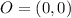`O= (0,0)` ---
`(x_1,y_1)`

`C = (1,0)` ---
`(x_2,y_2)`

`m : n = 4:1`

`E = ((4*1 + 1 * 0)/(4 + 1),(4*0 + 1*0)/(4 + 1))`

`E = ((4)/(5),(0)/(5))`

`E = (0.8,0)`