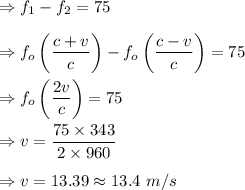Question

The security alarm on a parked car goes off and produces a frequency of 960 Hz. The speed of sound is 343 m/s. As you drive toward this parked car, pass it, and drive away, you observe the frequency to change by 75 Hz. At what speed are you driving

Answer 1

Answer:
`13.4\ m/s`

Step-by-step explanation:

Given

The frequency of the source is
`f_o=960\ Hz`

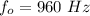
Change in frequency is
`75\ Hz`

Speed of sound
`c=343\ m/s`

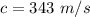
Suppose
`v` is the velocity of the observer

Doppler frequency is given by

`f'=f_o\left((c\pm v_o)/(c\pm v_s)\right)`

Here, the source is at rest

While approaching source, frequency is

`f_1=f_o\left((c+v)/(c)\right)\quad \ldots(i)`

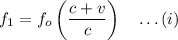
While leaving, frequency is

`f_2=f_o\left((c-v)/(c)\right)\quad \ldots(ii)`

The difference in the frequency is

`\Rightarrow f_1-f_2=75\\\\\Rightarrow f_o\left((c+v)/(c)\right)-f_o\left((c-v)/(c)\right)=75\\\\\Rightarrow f_o\left((2v)/(c)\right)=75\\\\\Rightarrow v=(75* 343)/(2* 960)\\\\\Rightarrow v=13.39\approx 13.4\ m/s`