Question

A hospital recorded the weights, in ounces, of newborn babies for two weeks. The

results are listed below.

Weights of babies born during week one: 128, 105, 80, 82, 96, 98, 87, 100, 112, 126

Weights of babies born during week two: 75, 85, 90, 97, 89, 105, 110, 127, 129, 130

Which statement is true?

Answer 1

The standard deviation for week two was about 3 ounces more than the standard deviation for week one

Explanation:

Given

`Week\ 1: 128, 105, 80, 82, 96, 98, 87, 100, 112, 126`

`Week\ 2: 75, 85, 90, 97, 89, 105, 110, 127, 129, 130`

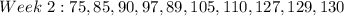
See attachment for options

Required

The true statement

Checking the standard deviation

For week 1

Calculate the mean:

`\bar x = (\sum x)/(n)`

`\bar x = (128+ 105+ 80+ 82+ 96+ 98+ 87+ 100+ 112+ 126)/(10)`

`\bar x = (1014)/(10)`

`\bar x_1 = 101.4`

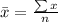
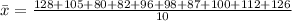
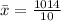
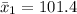
Then standard deviation

`\sigma = \sqrt{(\sum(x - \bar x)^2)/(n)}`

`\sigma_1 = \sqrt{((128 - 101.4)^2 +............+ (126- 101.4)^2)/(10)}`

`\sigma_1 = \sqrt{(2522.4)/(10)}`

`\sigma_1 = \sqrt{252.24`

`\sigma_1 = 15.88`

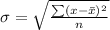
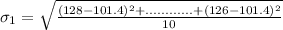
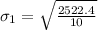
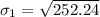
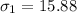
For week 2, we have:

`\bar x = (75+ 85+ 90+ 97+ 89+ 105+ 110+ 127+ 129+ 130)/(10)`

`\bar x = (1037)/(10)`

`\bar x_2 = 103.7`

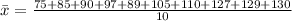
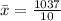
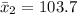
Then standard deviation

`\sigma_2 = \sqrt{((75 - 103.7)^2 +................+ (130- 103.7)^2)/(10)}`

`\sigma_2 = \sqrt{(3538.1)/(10)}`

`\sigma_2 = \sqrt{353.81`

`\sigma_2 = 18.81`

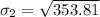
Compare the standard deviations

`\sigma_1 = 15.88`

`\sigma_2 = 18.81`

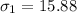
Calculate the difference:

`d = \sigma_2 - \sigma_1`

`d = 18.81 - 15.88`

`d = 2.93`

`d \approx 3`

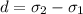
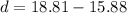
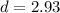
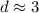
This implies that option (b) is true