Question

An engine flywheel initially rotates counterclockwise at 5.03 rotations/s. Then, during 23.5 s, its rotation rate changes to 2.63 rotations/s clockwise. Find the flywheel's average angular acceleration (including its sign) in radians per second squared. Define counterclockwise rotation as positive.

Answer 1

the flywheel's average angular acceleration is -2.05 rad/s²

Step-by-step explanation:

Note: counterclockwise is positive

clockwise is negative

Given;

initial angular velocity,
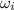`\omega _i` = 5.03 rev/s =
`5.03(rev)/(s) * (2\pi \ rad)/(1 \ rev) = 31.61 \ rad/s`

final angular velocity,
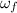`\omega_f`= -2.63 rev/s =
`-2.63 \ (rev)/(s) * (2\pi \ rad)/(1 \ rev) = -16.53 \ rad/s`

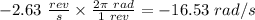
duration of the flywheel rotation, Δt = 23.5 s

The average acceleration of the flywheel is calculated as;

`a_r = (\Delta \omega)/(\Delta t) = (\omega_f - \omega _i)/(t_2-t_1) = (-16.53 \ - \ 31.61)/(23.5) = -2.05 \ rad/s^2`

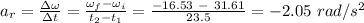
Therefore, the flywheel's average angular acceleration is -2.05 rad/s²