Question

A small airplane flies 1015 miles with an average speed of 290 miles per hour. 1.75 hours after the plane leaves, a Boeing 747 leaves from the same point. Both planes arrive at the same time; what was the average speed of the 747

Answer 1

The average speed of the 747 was of 580 miles per hour.

Explanation:

We use the following relation to solve this question:

`v = (d)/(t)`

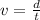
In which v is the velocity, d is the distance and t is the time.

A small airplane flies 1015 miles with an average speed of 290 miles per hour.

We have to find the time:

`v = (d)/(t)`

`290 = (1015)/(t)`

`290t = 1015`

`t = (1015)/(290)`

`t = 3.5`

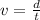
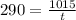
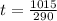
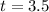
1.75 hours after the plane leaves, a Boeing 747 leaves from the same point. Both planes arrive at the same time;

The time of the Boeing 747 is:

`t = 3.5 - 1.75 = 1.75`

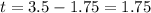
Distance of
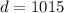`d = 1015`, the velocity is:

`v = (d)/(t) = (1015)/(1.75) = 580`

The average speed of the 747 was of 580 miles per hour.