Question

A sample of 28 sales transactions at Costco shows a mean transaction time of 296 seconds with a standard deviation of 48 seconds. Costco is interested in finding out whether the mean transaction time is less than 310 seconds. Answer the following questions. a) Write down the null and alternative hypotheses. b) Find the test statistic and the critical value at 1% significance level. c) At 1% level of significance, what is your conclusion

Answer 1

a) The null hypothesis is
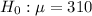`H_0: \mu = 310` and the alternative hypothesis is
`H_1: \mu < 310`.

b) The test statistic is
`t = -1.54`. The critical value is
`t_c = -2.473`.

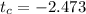c) The test statistic is
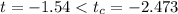`t = -1.54 < t_c = -2.473`, which means that there is not enough evidence to reject the null hypothesis that the mean transaction time is of 310 times, so no evidence to conclude that the mean transaction time is less than 310 seconds.

Explanation:

Question a:

Costco is interested in finding out whether the mean transaction time is less than 310 seconds.

At the null hypothesis, we test if the mean is of 310 seconds, that is:

`H_0: \mu = 310`

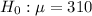
At the alternative hypothesis, we test if the mean is of less than 310 seconds, that is:

`H_1: \mu < 310`

b) Find the test statistic and the critical value at 1% significance level.

Test if the mean is less than a value, sample of 28, and standard deviation for the sample. Thus, we have a left-tailed t-test with 28 - 1 = 27 degrees of freedom and a 0.01 significance level, and the critical value is
`t_c = -2.473`.

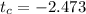The test statistic is:

`t = (X - \mu)/((s)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis, s is the standard deviation pf the sample and n is the size of the sample.

310 is tested at the null hypothesis:

This means that
`\mu = 310`.

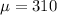A sample of 28 sales transactions at Costco shows a mean transaction time of 296 seconds with a standard deviation of 48 seconds.

This means that
`n = 28, X = 296, s = 48`.

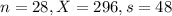Value of the test statistic:

`t = (X - \mu)/((s)/(√(n)))`

`t = (296 - 310)/((48)/(√(28)))`

`t = -1.54`

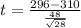
The test statistic is
`t = -1.54`.

c) At 1% level of significance, what is your conclusion

The test statistic is
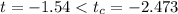`t = -1.54 < t_c = -2.473`, which means that there is not enough evidence to reject the null hypothesis that the mean transaction time is of 310 times, so no evidence to conclude that the mean transaction time is less than 310 seconds.