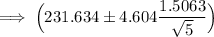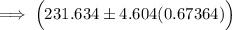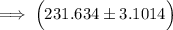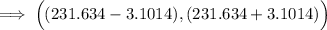Question

A journal article reports that a sample of size was used as a basis for calculating a CI for the true average natural frequency (Hz) of delaminated beams of a certain type. The resulting interval was . You decide that a confidence level of is more appropriate than the level used. What are the limits of the interval

Answer 1

The limit of the (228.533, 234.735)

Explanation:

The values are missing in the given question. Therefore, in order to attempt this question, we will make assumptions.

So, let's assume that:

sample size of the journal article that was reported = 5

which is applied for determining a 95% CI

Also, assuming that the resulting interval = (229.764, 233.504)

However, if we are to use a 99% CI which we deemed to be more appropriate;

Then, our objective is to find the limits of this particular interval in question.

To do that:

We need to first find the sample mean at 95% CI by using the formula:

`\Big ( \bar {x} - t_(\alpha/2, df) \ (s)/(√(n))}, \bar x + t_(\alpha/2, df) \ (s)/(√(n))} \Big) = (229.764,233.504)`

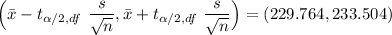
Since; df = n - 1

df = 5 - 1

df = 4

Then;

`\Big ( \bar {x} - t_(\alpha/2, 4) \ (s)/(√(n))}, \bar x + t_(\alpha/2, 4) \ (s)/(√(n))} \Big) = (233.504+229.764)`

`2 \bar {x} = (463.268)`

`\bar {x} =(463.268)/(2 )`

`\bar {x} =231.634`

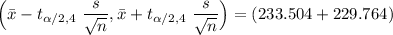
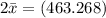
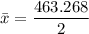
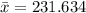
Sample mean = 231.634

Using the same formula to determine the standard deviation, we have:

`\Big ( \bar {x} - t_(\alpha/2, df) \ (s)/(√(n))}, \bar x + t_(\alpha/2, df) \ (s)/(√(n))} \Big) = (229.764,233.504)`

`\Big ( \bar {x} - t_(\alpha/2, 4) \ (s)/(√(n))}, \bar x + t_(\alpha/2, 4) \ (s)/(√(n))} \Big) = (233.504-229.764)`

`\Big ( (\bar x + t_(\alpha/2, 4) \ (s)/(√(n))} )- (\bar {x} - t_(\alpha/2, 4) \ (s)/(√(n))}) \Big) = (233.504-229.764)`

`\Big ( (\bar x + t_(0.05/2, 4) \ (s)/(√(4))} )- (\bar {x} - t_(0.05/2, 4) \ (s)/(√(5))}) \Big) = (233.504-229.764)`

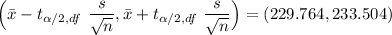
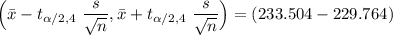
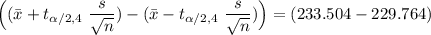
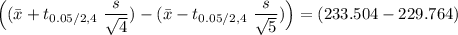
At t = 0.025 and df = 4; = 2.776

`2* 2.776 (s)/(√(5))= 3.74`

`5.552 (s)/(√(5))= 3.74`

`(s)/(√(5))= ( 3.74)/(5.552)`

`(s)/(√(5))= 0.6736`

`s = 0.6736 * √(5)`

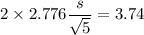
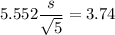
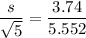
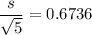
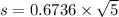
s = 1.5063

The 99% CI is:

`\implies \Big(\bar x \pm t_(\alpha/2,4) (s)/(√(n)) \Big)`

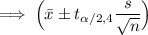
At t =0.005 and df =4; = 4.604

`\implies \Big(231.634 \pm 4.604 (1.5063)/(√(5)) \Big)`

`\implies \Big(231.634 \pm 4.604 (0.67364) \Big)`

`\implies \Big(231.634 \pm 3.1014 \Big)`

`\implies \Big((231.634 - 3.1014), (231.634 + 3.1014) \Big)`

`\implies \Big( 228.533, 234.735 \Big)`