Question

Maria plans to use fencing to build an enclosure or enclosures for her two horses. A single enclosure would be square shaped and require an area of 2,025 ft2. Two individual adjacent enclosures would be rectangular, with dimensions 20 ft by 40 ft with a 40 ft divider between the two enclosures. A square and a rectangle are shown. The square has an area of 2,025 feet squared. The rectangle is comprised of 2 rectangles that are 20 by 40 feet long. Which statement explains the design Maria should choose to minimize her costs

Answer 1

A

Explanation:

Answer 2

A. The singular enclosure would minimize cost because it requires 180 feet of fencing.

Explanation:

Given

Single enclosure

`Area = 2025ft^2` --- of square

Two adjacent enclosures

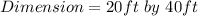`Dimension= 20ft\ by\ 40ft` ---- both rectangles

`Divider = 40ft`

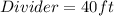
Required

Determine the true statement to minimize cost

Start by calculating the perimeter of the single enclosure.

Let

`l \to` length of the enclosure (square shape)

So:

`Area = l^2`

`2025 = l^2`

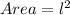
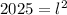
Rewrite as:

`l^2 = 2025`

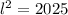
Take square roots

`l = 45`

The perimeter (P) is then calculated as:

`P = 4l`

`P = 4 * 45`

`P_1 = 180ft`

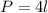
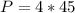
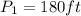
Next, the perimeter of the two enclosures.

Let

`l \to` length of the enclosure

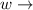`w \to` width of the enclosure

`l = 20`

`w =40`

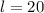
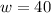
The perimeter of 1 enclosure is:

`P = 2(l + w)`

`P = 2(20 + 40)`

`P = 2*60`

`P = 120`

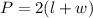
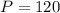
For 2 enclosures

`P_2 =2 * P`

`P_2 =2 * 120`

`P_2 =240`

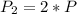
Remove the length of the divider

`P_2 = 240 - 40`

`P_2 = 200ft`

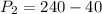
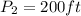
By comparison;

`P_1 < P_2`

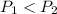
i.e.

`180ft < 200ft`

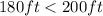
Hence, the singular enclosure will minimize costs