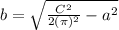Answer:
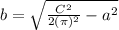
Explanation:
Given - The circumference of the ellipse approximated by
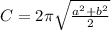 where 2a and 2b are the lengths of 2 the axes of the ellipse.
where 2a and 2b are the lengths of 2 the axes of the ellipse.
To find - Which equation is the result of solving the formula of the circumference for b ?
Solution -

Squaring Both sides, we get
![[(C)/(2\pi )]^(2) = [\sqrt{(a^(2) + b^(2) )/(2) }]^(2) \\(C^(2) )/((2\pi)^(2) ) = {(a^(2) + b^(2) )/(2) }\\2(C^(2) )/(4(\pi)^(2) ) = {{a^(2) + b^(2) }](https://img.qammunity.org/2022/formulas/mathematics/high-school/r7o4d8r7qh100eo6gk9hvja3403kkjv5o0.png)
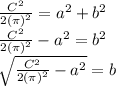
∴ we get