Answer:
2630 g
Explanation:
From the given information:
Given that:
mean (μ) = 3750 g
Standard deviation (σ) = 500
Suppose the hospital officials demand special treatment with a percentage of lightest 3% (0.03) for newborn babies;
Then, the weight of birth that differentiates the babies that needed special treatment from those that do not can be computed as follows;
P(Z < z₁) = 0.03
Using the Excel Formula; =NORMSINV(0.03) = -1.88
z₁ = - 1.88
Using the test statistics z₁ formula:
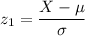
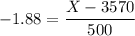
By cross multiply, we have:
-1.88 × 500 = X - 3570
-940 = X - 3570
-X = -3570 + 940
-X = -2630
X = 2630 g
Hence, 2630 g is the required weight of birth that differentiates the babies that needed special treatment from those that do not