Question

Could a polyhedron exist with the given number of faces, vertices, and edges? Drag yes or no to each combination

Answer 1

(a) No

(b) No

(c) No

Explanation:

Given

See attachment

Required

Select Yes or No for each

To do this, we make use of Euler's formula

`F + V - E = 2`

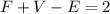
Where

`F \to Faces; V \to Vertices; E \to Edges`

`(a):\ Faces = 8; Vertices = 12; Edges = 6`

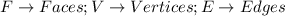
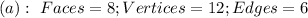
Using:
`F + V - E = 2`

`8 + 12 - 6 = 2`

`14 = 2`

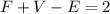
The above equality is false. Hence, (a) does not exist

`(b):\ Faces = 6; Vertices = 6; Edges = 4`

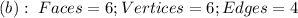
Using:
`F + V - E = 2`

`6 + 6 - 4 = 2`

`8 = 2`

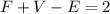
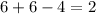
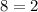
The above equality is false. Hence, (b) does not exist

`(c):\ Faces = 20; Vertices = 30; Edges = 12`

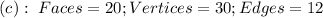
Using:
`F + V - E = 2`

`20 + 30 - 12 = 2`

`38 = 2`

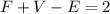
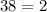
The above equality is false. Hence, (c) does not exist