Question

Which value(s) of x are solution(s) of the equation below

Answer 1

Hi there!

`\large\boxed{x = -1}`

We can solve by multiplying each term to get a common denominator:

`(1)/(x - 4) + (x)/(x - 2) = (2)/(x^2-6x+8)`

`(x -2)/((x - 4)(x - 2)) + (x(x - 4))/((x - 2)(x - 4)) = (2)/(x^2-6x+8)`

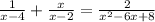
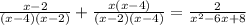
Since the denominators are all the same (x² - 6x + 8 factors to (x - 2)(x - 4)), we can ignore them temporarily and solve the numerator:

x - 2 + x(x - 4) = 2

Simplify:

x - 2 + x² - 4x = 2

x² - 3x - 4 = 0

Factor:

(x - 4)(x + 1) = 0

x = -1, 4

For the values of x to be a solution, they cannot cause the denominator to be equal to 0, so:

(x - 2)(x - 4) = 0

x = 2, 4. These values result in a denominator of 0, which is undefined.

Thus, the only solution is x = -1.