Answer:
Since
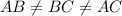 and
and
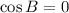 , we conclude that given triangle is a right-angled and scalene.
, we conclude that given triangle is a right-angled and scalene.
Explanation:
First, we determine the lengths of sides
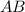 ,
,
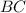 and
and
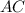 by the Equation of the Line Segment, which is based on the Pythagorean Theorem:
by the Equation of the Line Segment, which is based on the Pythagorean Theorem:
Line segment AB
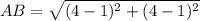
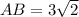
Line segment BC
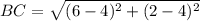
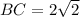
Line segment AC

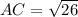
And the angles are found by means of the Law of Cosine:, where acute angles exist when
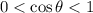 , whereas obtuse angles exist for
, whereas obtuse angles exist for
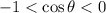 .
.
Angle A
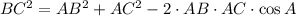 (1)
(1)

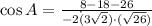

Angle B
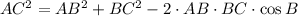 (2)
(2)
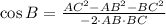
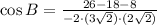
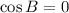
Angle C
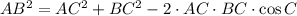 (3)
(3)
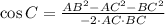
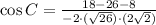
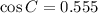
Since
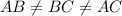 and
and
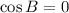 , we conclude that given triangle is a right-angled and scalene.
, we conclude that given triangle is a right-angled and scalene.