Question

Profit, P(x), is the difference between revenue, R(x), and cost, C(x), so P(x) = R(x) - CC). Which

expression represents P(x), if R(I) = 224 – 3x3 + 2x – 1 and C(x) = 24 – + 22 + 3?
3.14 - 31" - 22 + 4x + 2
** _ 3.7? _ 22 +42 + 2
I _ 313 + x² - 4
208_32
I NEED HELP ASAP

Answer 1

Explanation:

Profit, P(x), is the difference between revenue, R(x), and cost, C(x)

R(x) = 2x^4 - 3x^3 + 2x - 1

C(x) = x^4 -x^2 + 2x + 3

Substituting into the equation

P(x) = R(x) - C(x)

= (2x^4 - 3x^3 + 2x - 1) - (x^4 -x^2 + 2x + 3)

= x^4 - 3x^3 + x^2 - 4

The answer is the lower left option.

Answer 2

`P(x)=x^4-3x^3+x^2-4`

(This is the option found in the lower-left corner)

Explanation:

When given the following functions,

`R(x)=2x^4-3x^3+2x-1`

`C(x)=x^4-x^2+2x+3`

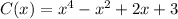
The problem asks one to find (
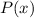`P(x)`), moreover, one is given the following information,

`(P(x))=(R(x))-(C(x))`

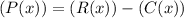
Substitute,

`P(x)=(2x^4-3x^3+2x-1)-(x^4-x^2+2x+3)`

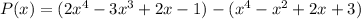
Simplify, multiply everything in the second parenthesis by the negative sign outside of it,

`P(x)=2x^4-3x^3+2x-1-x^4+x^2-2x-3`

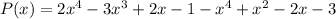
Combine like terms, only operations between coefficients of the same variable with the same degree (exponent) can be performed,

`P(x)=x^4-3x^3+x^2-4`