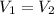Answer:
Equal volumes
Explanation:
Given
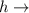 height of cone
height of cone
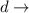 diameter of cone
diameter of cone
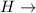 height of cylinder
height of cylinder
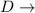 diameter of cylinder
diameter of cylinder
Such that:
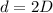

Required
The relationship between the volumes
The volume of a cylinder is:
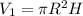
Where
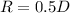
So:
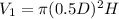


The volume of the cone is:
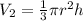
Where
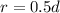

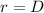
and

So, we have:
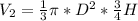



So, we have: