The inverse of f(x) is (option C)
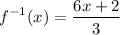
To find the inverse of the function
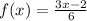 , we perform the following steps:
, we perform the following steps:
1. Swap x and y to express the inverse function:
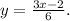
2. Solve for x : Multiply both sides by 6 to get rid of the fraction:
6y = 3x - 2 .
3. Add 2 to both sides:
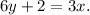
4. Divide by 3 to solve for x :
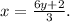
This gives us the inverse function
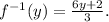 Simplifying the expression, we get:
Simplifying the expression, we get:
![\[ f^(-1)(y) = 2y + (2)/(3) \]](https://img.qammunity.org/2022/formulas/mathematics/college/cq774hd68lq9ujbuww3wbc459uaywnay8s.png)
Since this expression is in terms of y , to write it in the usual function form, replace y with x :
![\[ f^(-1)(x) = 2x + (2)/(3) \]](https://img.qammunity.org/2022/formulas/mathematics/college/3jkhsergdzi6cw8c24xj06m072c8gdronr.png)