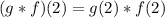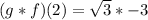Question

Drag the tiles to the boxes to form correct pairs.

Match each operation involving Rx) and g(x) to its answer.
(t) = 1 - 22 and g(x) = V11 — 41

Answer 1

`(g + f)(2) = \sqrt 3 - 3`

`((f)/(g))(-1) = 0`

`(g + f)(-1) = √(15)`

`(g * f)(2) = -3\sqrt 3`

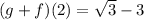
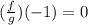
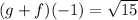
Explanation:

Given

`f(x) =1 - x^2`

`g(x) = \sqrt{11 - 4x`

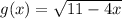
See attachment

Solving (a): (g + f)(2)

This is calculated as:

`(g + f)(2) = g(2) + f(2)`

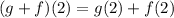
Calculate g(2) and f(2)

`g(2) \to √(11 - 4 * 2) = √(3)`

`f(2) = 1 - 2^2 = -3`

So:

`(g + f)(2) = g(2) + f(2)`

`(g + f)(2) = \sqrt 3 - 3`

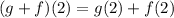
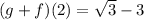
Solving (b):
`((f)/(g))(-1)`

This is calculated as:

`((f)/(g))(-1) = (f(-1))/(g(-1))`

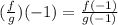
Calculate f(-1) and g(-1)

`f(-1) = 1 - (-1)^2 = 0`

So:

`((f)/(g))(-1) = (f(-1))/(g(-1))`

`((f)/(g))(-1) = (0)/(g(-1))`

`((f)/(g))(-1) = 0`

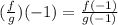
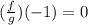
Solving (c): (g - f)(-1)

This is calculated as:

`(g + f)(-1) = g(-1) - f(-1)`

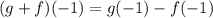
Calculate g(-1) and f(-1)

`g(-1) = √(11 - 4 * -1) = √(15)`

`f(-1) = 1 - (-1)^2 = 0`

So:

`(g + f)(-1) = g(-1) - f(-1)`

`(g + f)(-1) = √(15) - 0`

`(g + f)(-1) = √(15)`

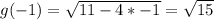
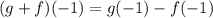
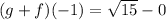
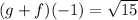
Solving (d): (g * f)(2)

This is calculated as:

`(g * f)(2) = g(2) * f(2)`

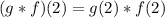
Calculate g(2) and f(2)

`g(2) \to √(11 - 4 * 2) = √(3)`

`f(2) = 1 - 2^2 = -3`

So:

`(g * f)(2) = g(2) * f(2)`

`(g * f)(2) = \sqrt 3 * -3`

`(g * f)(2) = -3\sqrt 3`