Answer:

Step-by-step explanation:
From the question we are told that:
Height
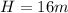
Radius

Height of water
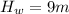
Gravity
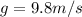
Density of water
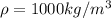
Generally the equation for Volume of water is mathematically given by
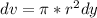
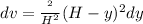
Where
y is a random height taken to define dv
Generally the equation for Work done to pump water is mathematically given by
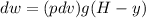
Substituting dv
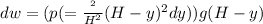
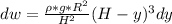
Therefore
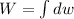
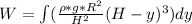
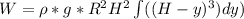
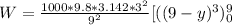
![W=3420.84*0.25[2401-65536]](https://img.qammunity.org/2022/formulas/physics/high-school/4bx3mv4k6lxuelpuoit6uu5bs5ua5lj356.png)
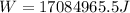

'
'