Answer:
There are two choices for angle Y:
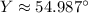 for
for
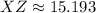 ,
,
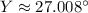 for
for
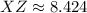 .
.
Explanation:
There are mistakes in the statement, correct form is now described:
In triangle XYZ, measure of angle X = 49°, XY = 18 and YZ = 14. Find the measure of angle Y:
The line segment XY is opposite to angle Z and the line segment YZ is opposite to angle X. We can determine the length of the line segment XZ by the Law of Cosine:
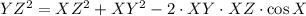 (1)
(1)
If we know that
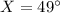 ,
,
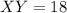 and
and
 , then we have the following second order polynomial:
, then we have the following second order polynomial:
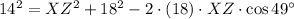
 (2)
(2)
By the Quadratic Formula we have the following result:
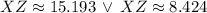
There are two possible triangles, we can determine the value of angle Y for each by the Law of Cosine again:
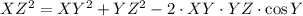
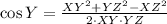
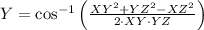
1)
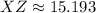
![Y = \cos^(-1)\left[(18^(2)+14^(2)-15.193^(2))/(2\cdot (18)\cdot (14)) \right]](https://img.qammunity.org/2022/formulas/mathematics/high-school/heqmtv2ff6zoib4cau4h1tj2p4tcko46of.png)
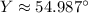
2)
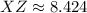
![Y = \cos^(-1)\left[(18^(2)+14^(2)-8.424^(2))/(2\cdot (18)\cdot (14)) \right]](https://img.qammunity.org/2022/formulas/mathematics/high-school/stncs11gf3dxfha7amsmdi2fgrz8bx72fm.png)
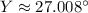
There are two choices for angle Y:
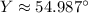 for
for
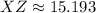 ,
,
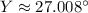 for
for
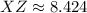 .
.