Given:
The expanded form of
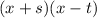 is
is
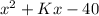 .
.
Where, s, t, K are positive integers.
To find:
The smallest possible value of K.
Solution:
The expanded form of
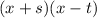 is
is
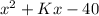 . It means,
. It means,
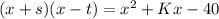
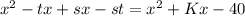
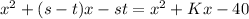
On comping both sides, we get
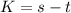 ...(i)
...(i)
K is a positive integer if s>t.
And
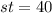
The factor pairs of 40 are (1,40), (2,20), (4,10), (5,8), (8,5), (10,4), (20,2) and (40,1).
Since s>t, therefore the possible values for (s,t) are (8,5), (10,4), (20,2) and (40,1).
Using (i), find the value of K for each factor pair.

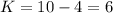


Therefore, the smallest possible value of K is 3.