Question

A hunter shoots a 500 g arrow at a 2.0 kg bird perched on a tall tree growing on flat, level ground. The arrow is launched from ground level with a speed of 40 m/s at an angle of 30 degrees above the horizon. It is traveling horizontally when it strikes and embeds in the bird. How far from the base of the tree do the bird and the arrow land

Answer 1

The bird and the arrow are 84.621 meters far from the hunter.

Step-by-step explanation:

The arrow experiments of a parabolic motion, which is the combination of horizontal motion at constant velocity and vertical uniform accelerated motion. The arrow strikes the bird when it reaches its maximum height. First, we determined the time taken by the arrow before striking the bird:

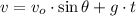`v = v_(o)\cdot \sin \theta + g\cdot t` (1)

Where:

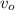`v_(o)` - Initial speed of the arrow, in meters per second.

`v` - Final speed of the arrow, in meters per second.

`\theta` - Launch angle, in sexagesimal degrees.

`g` - Gravitational acceleration, in meters per square second.

`t` - Time, in seconds.

If we know that
`v_(o) = 40\,(m)/(s)`,
`\theta = 30^(\circ)`,
`g = -9.807\,(m)/(s^(2))`,
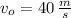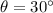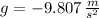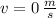`v = 0\,(m)/(s)`, then the time taken by the arrow is:

`t = (v-v_(o)\cdot \sin \theta)/(g)`

`t = (0\,(m)/(s)-\left(40\,(m)/(s)\right)\cdot \sin 30^(\circ) )/(-9.807\,(m)/(s^(2)) )`

`t = 2.039\,s`

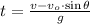
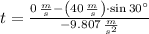
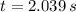
And the initial horizontal distance of the arrow (
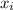`x_(i)`) is determined by this kinematic formula:

`x_(i) = (v_(o)\cdot \cos \theta)\cdot t` (2)

If we know that
`v_(o) = 40\,(m)/(s)`,
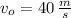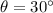`\theta = 30^(\circ)` and
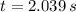`t = 2.039\,s`, then the initial horizontal distance is:

`x_(i) = \left[\left(40\,(m)/(s) \right)\cdot \cos 30^(\circ)\right]\cdot (2.039\,s)`

`x_(i) = 70.633\,m`

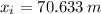
There is an inelastic collision between the arrow and the bird, the initial velocity of the bird-arrow system is:

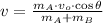`v = (m_(A)\cdot v_(o)\cdot \cos \theta)/(m_(A)+m_(B))` (3)

Where:

`v` - Initial velocity of the bird-arrow system, in meters per second.

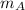`m_(A)` - Mass of the arrow, in kilograms.

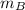`m_(B)` - Mass of the bird, in kilograms.

If we know that
`m_(A) = 0.5\,kg`,
`m_(B) = 2\,kg`,
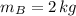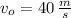`v_(o) = 40\,(m)/(s)` and
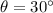`\theta = 30^(\circ)`, then the initial velocity of the bird-arrow system is:

`v = ((0.5\,kg)\cdot \left(40\,(m)/(s) \right)\cdot \cos 30^(\circ))/(0.5\,kg + 2\,kg)`

`v = 6.928\,(m)/(s)`

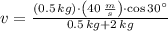
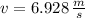
And the maximum height reached by the arrow (
`y`), in meters, is:

`y = y_(o) + (v_(o)\cdot \sin \theta)\cdot t +(1)/(2)\cdot g\cdot t^(2)` (4)

Where
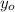`y_(o)` is the initial height of the arrow, in meters.

If we know that
`y_(o) = 0\,m`,
`v_(o) = 40\,(m)/(s)`,
`\theta = 30^(\circ)`,
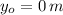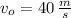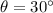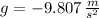`g = -9.807\,(m)/(s^(2))` and
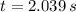`t = 2.039\,s`, then the maximum height reached by the arrow is:

`y = 0\,m + \left(40\,(m)/(s) \right)\cdot (2.039\,s)\cdot \sin 30^(\circ) +(1)/(2)\cdot \left(-9.807\,(m)/(s^(2))\right)\cdot (2.039\,s)^(2)`

`y = 20.394\,m`

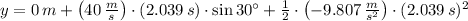
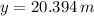
Time needed by the bird-arrow system to land is determined by this expression based on (4):

`y = y_(o) + (v_(o,y))\cdot t +(1)/(2)\cdot g\cdot t^(2)`

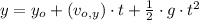
If we know that
`y_(o) = 20.394\,m`,
`y = 0\,m`,
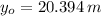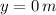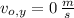`v_(o,y) = 0\,(m)/(s)` and
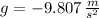`g = -9.807\,(m)/(s^(2))`, then the time needed to land is:

`0\,m = 20\,m + \left(0\,(m)/(s) \right)\cdot t + (1)/(2)\cdot \left(-9.807\,(m)/(s^(2)) \right)\cdot t^(2)`

`t = 2.019\,s`

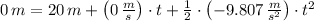
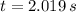
And the horizontal distance travelled by the bird-arrow system (
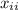`x_(ii)`), in meters, is calculated from a formula based on (2):

`x_(ii) = v_(o, x)\cdot t`

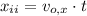
If we know that
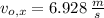`v_(o,x) = 6.928\,(m)/(s)` and
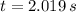`t = 2.019\,s`, then the distance travelled by the bird-arrow system is:

`x_(ii) = \left(6.928\,(m)/(s) \right)\cdot (2.019\,s)`

`x_(ii) = 13.988\,m`

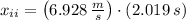
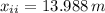
The final distance of the bird-arrow system from the hunter is:

`x = x_(i) + x_(ii)`

`x = 70.633\,m + 13.988\,m`

`x = 84.621\,m`

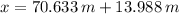
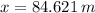
The bird and the arrow are 84.621 meters far from the hunter.