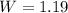Question

A school is planning to construct two rectangular play areas in the playground. The length of play area A must be 1 foot longer than four times its width. The width of play area B must be 2 feet longer than the width of play area A, and the length must be 2 feet longer than three times its own width. In addition, the areas of the two play areas must be equal. Write a system of equations to represent this situation, where y is the area of the play areas and x is the width of play area A. Which statement describes the number and viability of the system's solutions?

Answer 1

А.The system has two solutions, but only one is viable because the other results in a negative width.

Explanation:

Given

Let:

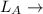`L_A \to` length of play area A

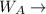`W_A \to` width of play area A

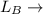`L_B \to` length of play area B

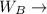`W_B \to` width of play area B

`x \to` Area of A

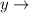`y \to` Area of B

From the question, we have the following:

`L_A = 1 + 4W_A`

`W_B = 2 + W_A`

`L_B = 2 + 3W_B`

`x = y`

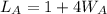
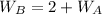
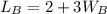
The area of A is:

`x = L_A * W_A`

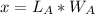
This gives:

`x = (1 + 4W_A) * W_A`

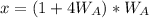
Open bracket

`x = W_A + 4W_A^2`

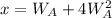
The area of B is:

`y = L_B * W_B`

`y = (2 + 3W_B) * ( 2 + W_A)`

Substitute:
`W_B = 2 + W_A`

`y = (2 + 3(2 + W_A)) * ( 2 + W_A)`

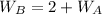
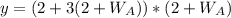
Open brackets

`y = (2 + 6 + 3W_A) * ( 2 + W_A)`

`y = (8 + 3W_A) * ( 2 + W_A)`

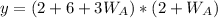
Expand

`y = 16 + 8W_A + 6W_A + 3W_A^2`

`y = 16 + 14W_A + 3W_A^2`

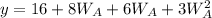
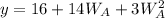
We have that:

`x = y`

This gives:

`W_A + 4W_A^2 = 16 + 14W_A + 3W_A^2`

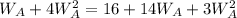
Collect like terms

`4W_A^2 - 3W_A^2 + W_A -14W_A - 16 =0`

`W_A^2 -13W_A - 16 =0`

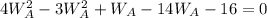
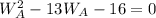
Using quadratic calculator, we have:

`W_A = -14.1` or
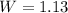`W = 1.13` --- approximated

But the width can not be negative; So:

`W = 1.19`