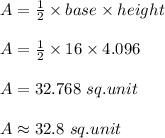Question

Find answer on the attached work sheet please there are 2 answers

Answer 1

The altitude is 4.1

The area of triangle DEF is 32.8

Explanation:

An altitude drawn from angle F to the opposite side of the triangle will intercept length DE.

let the altitude = h

Apply trig-ratio to determine the value of the altitude "h";

`sin (55) = (h)/(FE) \\\\sin (55) = (h)/(5) \\\\h = 5 * sin(55)\\\\h = 5(0.8192)\\\\h = 4.096`

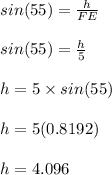
The area of ΔDEF using the value of the altitude is calculated as;

`A = (1)/(2) * base * height\\\\A = (1)/(2) * 16 * 4.096\\\\A = 32.768 \ sq.unit\\\\A \approx 32.8 \ sq.unit`