Find the side lengths of the triangle in this picture.

Question

asked Dec 9, 2022 206k views

1 Answer

Tempuslight · Answer 1 · 2022-12-13T17:01:53+0000

Answer:

Hypotenuse: 41 meters, Long leg: 40 meters, Short leg: 9 meters.

Explanation:

According to the statement, we have the following information about the lengths of the right triangle:

Hypotenuse

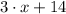
$3\cdot x + 14$

Long leg

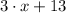
$3\cdot x + 13$

Short leg

By the Pythagoric Theorem, we have the following expression:

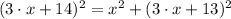$(3\cdot x + 14)^(2) = x^(2) + (3\cdot x + 13)^(2)$ (1)

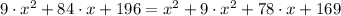
$9\cdot x^(2)+84\cdot x + 196 = x^(2) + 9\cdot x^(2) + 78\cdot x + 169$

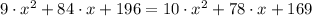
$9\cdot x^(2) + 84\cdot x + 196 = 10\cdot x^(2) + 78\cdot x +169$

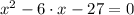
$x^(2) -6\cdot x -27 = 0$

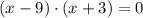
$(x-9)\cdot (x+3) = 0$

As length is a positive variable by nature, then the only possible solution is
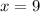x = 9 . Lastly, the side lengths of the right triangle are:

Hypotenuse: 41 meters, Long leg: 40 meters, Short leg: 9 meters.