Answer:
The triangle EFG can be constructed with the following specifications:
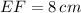 ,
,
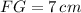 ,
,
 ,
,
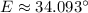 ,
,
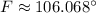 ,
,
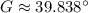 .
.
Explanation:
A triangle is formed by either knowing the lengths of its three sides or knowing two angles and the length of a side or knowing a angle and the lengths of two sides. By Geometry, we know that sum of internal angles in triangles equals 180°. In order to construct this triangle, we need to know the measures of angles E, F and G by means of the Law of Cosine:
Angle E
![E = \cos^(-1)\left[((7\,cm)^(2)-(12\,cm)^(2)-(8\,cm)^(2))/(-2\cdot (12\,cm)\cdot (8\,cm)) \right]](https://img.qammunity.org/2022/formulas/mathematics/high-school/p08pjranynk1mjv67qp9om5d6s2kluvrkr.png)
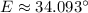
Angle F
![F = \cos^(-1)\left[((12\,cm)^(2) - (8\,cm)^(2) - (7\,cm)^(2))/(-2\cdot (8\,cm)\cdot (7\,cm)) \right]](https://img.qammunity.org/2022/formulas/mathematics/high-school/6mdahwlosz3wjkal0pvuxxsngud8pavvnc.png)
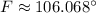
Angle G
![G = \cos^(-1)\left[((8\,cm)^(2)-(12\,cm)^(2)-(7\,cm)^(2))/(-2\cdot (12\,cm)\cdot (7\,cm)) \right]](https://img.qammunity.org/2022/formulas/mathematics/high-school/qn2hneq6e5dxou1uajo60swq8ff0hxwbcy.png)
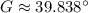
The triangle EFG can be constructed with the following specifications:
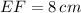 ,
,
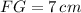 ,
,
 ,
,
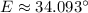 ,
,
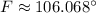 ,
,
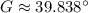 .
.