Answer:
The height of the tree in 2020 was of 19.63 feet.
Explanation:
Exponential equation for growth:
The exponential equation for the growth of an amount has the following format:
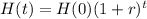
In which H(t) is the amount after t years, H(0) is the initial amount and r is the growth rate, as a decimal.
A 4 foot tree was planted in 2012 outside a high school.
This means that
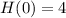
The tree grew continuously by 22% each year from that point.
This means that

Find out what the height of the tree was in 2020.
2020 is 2020 - 2012 = 8 years after 2012, so this is H(8).
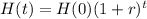
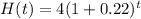
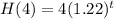
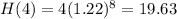
The height of the tree in 2020 was of 19.63 feet.