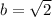Answer:
(1)
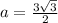

(2)
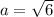
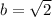
Explanation:
Solving (1):
Considering
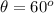
We have:
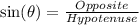
This gives:
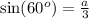
Solve for a
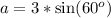
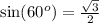
So:
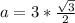
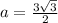
To solve for b, we make use of Pythagoras theorem
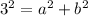
This gives
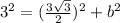


Collect like terms
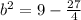
Take LCM and solve
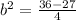
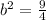
Take square roots

Solving (2):
Considering
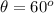
We have:
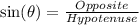
This gives:

Solve for a
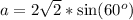
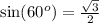
So:
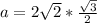

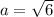
To solve for b, we make use of Pythagoras theorem
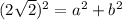
This gives
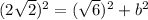
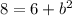
Collect like terms
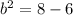

Take square roots