Answer:
a)
The null hypothesis is
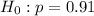 .
.
The alternate hypothesis is
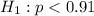 .
.
The decision rule is: accept the null hypothesis for
 , reject the null hypothesis for
, reject the null hypothesis for
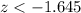 .
.
Since
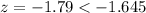 , we reject the null hypothesis and accept the alternate hypothesis that that percentage of athletes who graduate is less than for the student population at large.
, we reject the null hypothesis and accept the alternate hypothesis that that percentage of athletes who graduate is less than for the student population at large.
b)
The p-value for this test is 0.0367. Since this p-value is less than the significance level of
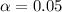 , we reject the null hypothesis and accept the alternate hypothesis that that percentage of athletes who graduate is less than for the student population at large.
, we reject the null hypothesis and accept the alternate hypothesis that that percentage of athletes who graduate is less than for the student population at large.
Explanation:
Question a:
Perform the appropriate hypothesis test to determine whether this is significant evidence that the percentage of athletes who graduate is less than for the student population at large:
At the null hypothesis, we test if the proportion is the same as the student population, of 91%. Thus:
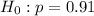
At the alternate hypothesis, we test that the proportion for athletes is less than 91%, that is:
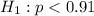
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
Test if the proportion is less at the 0.05 level:
The critical value is z with a p-value of 0.05, that is, z = -1.645. Thus, the decision rule is: accept the null hypothesis for
 , reject the null hypothesis for
, reject the null hypothesis for
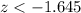 .
.
0.91 is tested at the null hypothesis:
This means that

A sports reporter contacted 152 athletes randomly sampled from that same university and time period and found that 132 of them had graduated within 6 years.
This means that
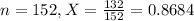
Value of the test statistic:

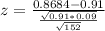
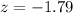
Since
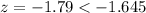 , we reject the null hypothesis and accept the alternate hypothesis that that percentage of athletes who graduate is less than for the student population at large.
, we reject the null hypothesis and accept the alternate hypothesis that that percentage of athletes who graduate is less than for the student population at large.
(b) (3 points) Calculate the P-value for this test. Explain how this P-value can be use to test the hypotheses in part (a).
The p-value of the test is the probability of finding a sample proportion of 0.8684 or below. This is the p-value of z = -1.79.
Looking a the z-table, z = -1.79 has a p-value of 0.0367.
The p-value for this test is 0.0367. Since this p-value is less than the significance level of
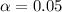 , we reject the null hypothesis and accept the alternate hypothesis that that percentage of athletes who graduate is less than for the student population at large.
, we reject the null hypothesis and accept the alternate hypothesis that that percentage of athletes who graduate is less than for the student population at large.