Question

Find the domain and range of f(x). Please explain your answer.
f(x) = √(x^2+5x+6)

Answer 1

Domain:— [ x ≥ -2, x ≤ -3 ]

Range:— [ y ≥ 0 ]

Explanation:

You may use graphing calculator to draw a graph and examine the graph’s domain and range. However, I’ll explain further about the graph of quadratic in a surd.

First, factor the quadratic expression in the surd:—

`\displaystyle \large{f(x)=√((x+3)(x+2))}`

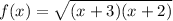
We can find the x-intercepts by letting f(x) = 0.

I’ll be separating in two parts — one for finding x-intercept and one for finding y-intercept.

__________________________________________________________

Finding x-intercepts

Let f(x) = 0.

`\displaystyle \large{0=√((x+3)(x+2))}`

Solve for x, square both sides:—

`\displaystyle \large{0^2 = (√((x+3)(x+2)))^2}\\\displaystyle \large{0=(x+3)(x+2)}`

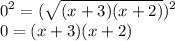
Simply solve a quadratic equation:—

`\displaystyle \large{x=-3,-2}`

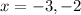
Therefore, x-intercepts are:—

`\displaystyle \large{\boxed{x=-3,-2}}`

__________________________________________________________

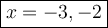
Finding y-intercept

Let x = 0.

`\displaystyle \large{f(x)=√((0+3)(0+2))}\\\displaystyle \large{f(x)=√(3 \cdot 2)}\\\displaystyle \large{f(x)=√(6)}`

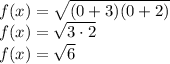
Therefore, y-intercept is:—

`\displaystyle \large{\boxed{√(6)}}`

__________________________________________________________

However, I want you to focus on x-intercepts instead. We know that the square root only gives you a positive value. That means the range of function can only be y ≥ 0.

For domain, first, we have to know how or what the graph looks like. You can input the function in a graphing calculator as you’ll see that when x ≥ -2, the graph heads to the right while/when x ≤ -3, the graph heads to the left. This means that the lesser value of x-intercept gets left and more value get right.

See, between -3 < x < -2, there is no curve, point or anything between the interval. Therefore, -3 < x < -2 does not exist in function.

Hence, the domain is:—

x ≥ -2, x ≤ -3