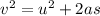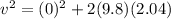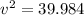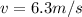Question

a 2.5kg mass is held above the ground and has 50 J of gravitational potential energy. the mass is then dropped and accelerates to the ground. find the speed that the mass has when it collides with the ground

Answer 1

`6.3m/s`

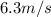
Explanation:

Note: We will take g as 9.8 in this question.

The two equations we will use for this questions are:

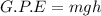`G.P.E = mgh`, m = mass, g = acceleration due to gravity

and the SUVAT equation:
`v^2=u^2+2as`

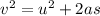
First, let's start out by finding the height from which the object is being dropped. We can do this by using the gravitational potential energy formula.

Subbing the values we have:

`50 = 2.5*9.8*h`

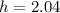`h = 2.04` - re-arranging for the height we get a height of 2.04.

Now we will use the SUVAT equation. Let's set out the variables we have:

`S=2.04\\U=0\\V=?\\A=9.8\\T=N/A`

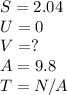
U (initial speed) is equal to 0 because we are dropping the object from rest. Acceleration is equal to 9.8 as that is the acceleration due to gravity. The displacement (S) is the height we just worked out.

Now let's put them into one of the SUVAT equations:

`v^2=u^2+2as`

`v^2=(0)^2+2(9.8)(2.04)`

`v^2=39.984`

`v=6.3 m/s`